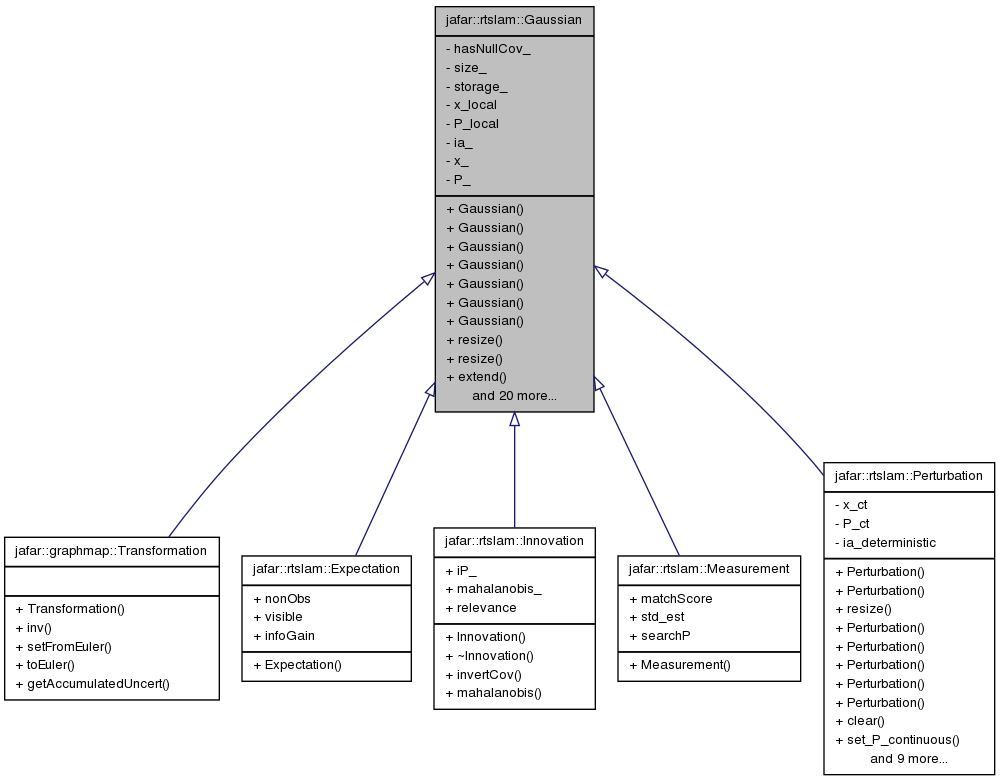
Class for Gaussians having LOCAL or REMOTE storage. More...

Detailed Description

Class for Gaussians having LOCAL or REMOTE storage.

Author:: jsola & croussil

This class defines a multi-dimensional Gaussian variable. It allows mean and covariances data to be stored locally or remotelly, depending on the constructor (the storage modality is selectable only at construction time). Remote Gaussians are indexed with indirect arrays.

Mean and covariances are accessed through x() and P().
The indirect array is part of the Gaussian class, and is accessible through ia().

HELP: For information about indirect arrays, see the documentation of ia_range(), ia_head() and similar functions in namespace jafar::jmath::ublasExtra.

To construct a local Gaussian

You just give a size, a pair {x , P } or another Gaussian:

 Gaussian GLa(7);                     // Construct from size.
 Gaussian GLb(x);                     // Construct from vector.
 Gaussian GLc(x, P);                  // Construct from given vector and matrix.
 Gaussian GLd(GL);                    // Copy-construct from local Gaussian.
 Gaussian GLe(GR, Gaussian::LOCAL);   // Copy-construct from remote, force local storage.

You can create Gaussians with no covariance by providing just the mean vector. This is only possible for local Gaussians. The Gaussian GLb above is an example.

See that the last constructor GLe takes a remote Gaussian (see below). The directive Gaussian::LOCAL tells the constructor to force local storage. The result is a local Gaussian (the data is copied to the local storage).

To construct a remote Gaussian

Remote Gaussians always point to local Gaussians (or to explicit {x,P} data):

 Gaussian GRa(GR);                    // Copy a remote Gaussian
 Gaussian GRb(GL, Gaussian::REMOTE);  // Point to a whole local Gaussian
 Gaussian GRc(x, P, ia);              // Point to a part of given x and P.
 Gaussian GRd(GL, ia);                // Point to a part of a given local Gaussian
 Gaussian GRe(GR, ia);                // Point to a part of a given remote Gaussian

In the first case, GRa points to the same Gaussian as GR.

In the second case, the directive Gaussian::REMOTE tells the constructor not to copy GL (as in GLd above) but to create a remote Gaussian that points to GL.

In the last three constructor modes, the produced Gaussian points to just a sub-set of the provided data. Specify the set of indices to the provided data with an indirect array jblas::ind_array .

REMEMBER: remote Gaussians always point to local Gaussians. See that the remote constructor GRe accepts a remote Gaussian GR to point to. In this case, the created Gaussian GRe is set to point to the local Gaussian GR was pointing to, say GL, and its indirect array is composed accordingly (composed means that after creation we have GRe.ia(i) = GR.ia(ia(i)), that is, the resulting GR.ia is different from the provided one ia). The reference to GR is therefore lost.

Managing cross-variances through indirect indexing

Having two remote Gaussian instances G1 and G2 pointing to the same data (Gaussian G or pair {x , P }) allows recovering their cross-variances matrix.

You can recover a hard copy of the cross-variance block with one of these:

 mat c = project(  P  , G1.ia(), G2.ia());
 mat c = project(G.P(), G1.ia(), G2.ia());

You can have an indirect access to the cross-variance block with one of these:

 sym_mat_indirect ic(  P  , G1.ia(), G2.ia());
 sym_mat_indirect ic(G.P(), G1.ia(), G2.ia());

This is a graphical representation of the situation, where we want to access the blocks of data ic and ic' (in purple):

Two remote Gaussians G1 and G2 pointing to {x, P } via indirect arrays. The cross-variances ic and ic' are shown.

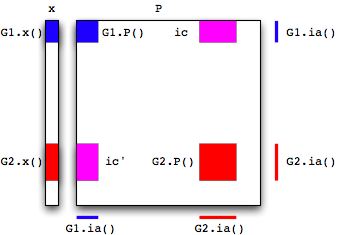
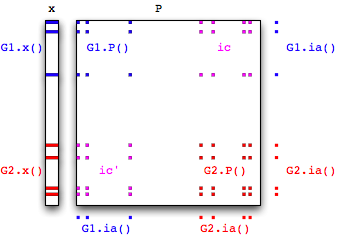
Bear in mind that indirect arrays are not correlative: they contain sparse indices. Thus this is a more accurate representation of the situation:

Two remote Gaussians G1 and G2 pointing to {x, P } via indirect arrays. The cross-variances ic and ic' are shown.

The following example shows the recovery and manipulation of the cross-variance. It is borrowed from test_gaussian02() in file rtslam/test_suite/test_gaussian.cpp:

  jblas::vec x(300);                                      // The remote mean vector.
  jblas::sym_mat P(300);                                  // The remote covariances matrix.
  P(1,102) = 99;                                          // We put here a value to test later
  Gaussian G1(x, P, ublasExtra::ia_range(0, 3));          // G1 points to positions {0, 1, 2}.
  Gaussian G2(x, P, ublasExtra::ia_range(100, 104));      // G2 points to positions {100, 101, 102, 103}.
  jblas::mat c = ublas::project(P, G1.ia(), G2.ia());     // Cross-variance (hard copy)
  jblas::sym_mat_indirect ic(P, G1.ia(), G2.ia());        // Cross-variance (indirectly indexed)
  cout << " c-value (should be 99): " << c(1,2) << endl;  // We recover here the values
  cout << "ic-value (should be 99): " << ic(1,2) << endl; //
  P(1,102) = 0;                                           // We change the P-value to test ic
  cout << " c-value (should be 99): " << c(1,2) << endl;  // We recover here the values
  cout << "ic-value (should be 0 ): " << ic(1,2) << endl; //

which renders the output:

 >>  c-value (should be 99): 99
 >> ic-value (should be 99): 99
 >>  c-value (should be 99): 99
 >> ic-value (should be 0 ): 0

Run this test yourself. Follow these steps :

edit rtslam/test_suite/test_gaussian.cpp
go to the bottom of the file, locate the macro function BOOST_AUTO_TEST_CASE( test_gaussian )
in this macro, comment all but test_gaussian02(). Save the file.
cd to directory $JAFAR_DIR/modules/rtslam/
type make test_gaussian
Once you are done, recover the file to its original state.

Definition at line 173 of file gaussian.hpp.

#include <gaussian.hpp>

Inheritance diagram for jafar::rtslam::Gaussian:

[legend]

List of all members.

Public Types
enum	storage_t { REMOTE, LOCAL, UNCHANGED }
	Storage type of Gaussians: LOCAL, REMOTE. More...
Public Member Functions
	Gaussian (const size_t _size)
	Local constructor from size.
	Gaussian (const jblas::vec &_x)
	Local constructor from mean data, no covariance.
	Gaussian (const jblas::vec &_x, const jblas::sym_mat &_P)
	Local constructor from full data.
	Gaussian (const Gaussian &G, storage_t _storage=UNCHANGED)
	Flexible copy constructor.
	Gaussian (Gaussian &G, const jblas::ind_array &_ia)
	Remote constructor from Gaussian.
	Gaussian (jblas::vec &_x, jblas::sym_mat &_P, const jblas::ind_array &_ia)
	Remote constructor from data.
void	resize (size_t n, bool preserve=true)
void	resize (const jblas::ind_array &_ia)
void	extend (size_t n)
void	extend (const jblas::ind_array &_ia)
bool	hasNullCov () const
storage_t	storage () const
size_t	size () const
jblas::ind_array &	ia ()
const jblas::ind_array &	ia () const
jblas::vec_indirect &	x ()
const jblas::vec_indirect &	x () const
jblas::sym_mat_indirect &	P ()
const jblas::sym_mat_indirect &	P () const
double &	x (size_t i)
double &	P (size_t i, size_t j)
void	storage (const storage_t &_s)
void	hasNullCov (bool _hasNullCov)
void	x (const jblas::vec &_x)
void	P (const jblas::sym_mat &_P)
void	std (const jblas::vec &_std)
	Set covariances matrix from standard deviations vector.
void	std (double _std)
	Set covariances matrix from standard deviation scalar value.
void	P (const jblas::mat &M, const jblas::ind_array &ia1, const jblas::ind_array &ia2)
	Set off-diagonal block in the covariances matrix.
virtual void	clear (void)
	Clear data, keep sizes and ranges.
double	probabilityDensity (const jblas::vec &v) const
	Probability density.
Private Attributes
bool	hasNullCov_
	true if covariance is exactly null
std::size_t	size_
	size of data
storage_t	storage_
	select local or remote storage
jblas::vec	x_local
	local storage mean
jblas::sym_mat	P_local
	local storage covariance
jblas::ind_array	ia_
	indirect array of indices to storage
jblas::vec_indirect	x_
	indexed mean
jblas::sym_mat_indirect	P_
	indexed covariance
Friends
std::ostream &	operator<< (std::ostream &s, Gaussian const &g_)
	Operator << for class Gaussian.

Member Enumeration Documentation

enum jafar::rtslam::Gaussian::storage_t

Storage type of Gaussians: LOCAL, REMOTE.

Enumerator:

REMOTE	Mean and covariances point to an external pair {x,P}.
LOCAL	Mean and covariances are stored in x_local and P_local.
UNCHANGED	Used only as the default flag for the copy constructor.

Definition at line 178 of file gaussian.hpp.

Constructor & Destructor Documentation

jafar::rtslam::Gaussian::Gaussian ( const size_t _size ) [inline]

Local constructor from size.

This constructor defines a local-storage Gaussian of size _size. Data is cleared automatically.

Parameters:

_size the size of the Gaussian.

Definition at line 225 of file gaussian.hpp.

References clear(), ia_, and size_.

jafar::rtslam::Gaussian::Gaussian ( const jblas::vec & _x ) [inline]

Local constructor from mean data, no covariance.

This constructor stores the input information in the local storage x_local. This data is accessed through x().

Parameters:

_x	the Gaussian mean.

Definition at line 265 of file gaussian.hpp.

References ia_, and size_.

jafar::rtslam::Gaussian::Gaussian	(	const jblas::vec &	_x,
		const jblas::sym_mat &	_P
	)		`[inline]`

Local constructor from full data.

This constructor stores the input information in the local storage x_local and P_local. This data is accessed through x() and P().

Parameters:

_x	the Gaussian mean.
_P	the Gaussian covariances matrix.

Definition at line 287 of file gaussian.hpp.

References ia_, JFR_ASSERT, and size_.

jafar::rtslam::Gaussian::Gaussian	(	const Gaussian &	G,
		storage_t	_storage = `UNCHANGED`
	)		`[inline]`

Flexible copy constructor.

Called with Gaussian(G) is a copy constructor.
Called with Gaussian(G, UNCHANGED) is also a copy constructor.
Called with Gaussian(G, LOCAL) forces the created Gaussian to have local storage.
Called with Gaussian(G, REMOTE) forces the created Gaussian to have remote storage.

Parameters:

G	the Gaussian to copy.
_storage	the directive to force local or remote storage.

Definition at line 314 of file gaussian.hpp.

jafar::rtslam::Gaussian::Gaussian	(	Gaussian &	G,
		const jblas::ind_array &	_ia
	)		`[inline]`

Remote constructor from Gaussian.

This constructor uses indirect indexing onto the Gaussian provided to the constructor. The indirect array where this new Gaussian points to in the old one is also given as input.

In case the input Gaussian is REMOTE, a composition of indirect arrays is performed, and the resulting Gaussian points to the Gaussian where the remote Gaussian points to.

The local storage x_local and P_local in the constructed Gaussian are kept at null size for economy.

Parameters:

G	a Gaussian.
_ia	an indirect array of indices pointing to G.

Definition at line 358 of file gaussian.hpp.

jafar::rtslam::Gaussian::Gaussian	(	jblas::vec &	_x,
		jblas::sym_mat &	_P,
		const jblas::ind_array &	_ia
	)		`[inline]`

Remote constructor from data.

This constructor uses indirect indexing onto a remote pair {_x, _P} provided to the constructor. The indirect array where this new Gaussian points to in {_x, _P} is also given as input. For practical use, the result is such that the new Gaussian Gnew has x_ = _x(_ia) and P_ = _P(_ia,_ia). The local storage x_local and P_local is kept at null size for economy.

Parameters:

_x	the remote mean vector.
_P	the remote covariances matrix.
_ia	the indirect array.

Definition at line 401 of file gaussian.hpp.

References JFR_ASSERT.

Member Function Documentation

virtual void jafar::rtslam::Gaussian::clear ( void ) [inline, virtual]

Clear data, keep sizes and ranges.

Clears the data of x_ and P_.

Reimplemented in jafar::rtslam::Perturbation.

Definition at line 541 of file gaussian.hpp.

References P_, size_, and x_.

Referenced by jafar::rtslam::Perturbation::clear(), and Gaussian().

void jafar::rtslam::Gaussian::P	(	const jblas::mat &	M,
		const jblas::ind_array &	ia1,
		const jblas::ind_array &	ia2
	)		`[inline]`

Set off-diagonal block in the covariances matrix.

Only works for local Gaussians.

Parameters:

M	the off-diagonal block.
ia1	the indirect array for rows.
ia2	the indirect array for columns.

Definition at line 532 of file gaussian.hpp.

References P_local.

double jafar::rtslam::Gaussian::probabilityDensity ( const jblas::vec & v ) const

Probability density.

Parameters:

v	the evaluation point

void jafar::rtslam::Gaussian::std ( const jblas::vec & _std ) [inline]

Set covariances matrix from standard deviations vector.

Parameters:

std	the vector of standard deviations.

Definition at line 504 of file gaussian.hpp.

References JFR_ASSERT, P_, and size_.

void jafar::rtslam::Gaussian::std ( double _std ) [inline]

Set covariances matrix from standard deviation scalar value.

Parameters:

std	the standard deviation.

Definition at line 517 of file gaussian.hpp.

References P_, and size_.

Friends And Related Function Documentation

std::ostream& operator<<	(	std::ostream &	s,
		Gaussian const &	g_
	)		`[friend]`

Operator << for class Gaussian.

It shows different information depending on the Gaussian having local or remote storage. For local storage, the mean and covariance data is shown. For remote storage, the size of the remote Gaussian is also shown, and the indirect array too.

Definition at line 559 of file gaussian.hpp.

The documentation for this class was generated from the following file:

modules/rtslam/include/rtslam/gaussian.hpp

Detailed Description

Public Types

Public Member Functions

Private Attributes

Friends

Member Enumeration Documentation

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation